Gradient Descent (梯度下降)
梯度下降(Gradient Descent)是一种用于优化目标函数的迭代算法,广泛应用于机器学习和深度学习中,用于训练模型以最小化损失函数。推荐先阅读 机器学习基础 文章以对梯度下降的背景有大概的了解。
目标函数
目标函数 (Objective Function):有时也称作准则(criterion)、代价函数(cost function)或损失函数(loss function),是我们希望最小化的函数,通常表示为 $J(\theta)$,其中 $\theta$ 是模型的参数。例如,在线性回归中使用的 均方误差 (Mean Squared Error, MSE) 就是一个常见的目标函数。
一般来说,定义 $x^* = \arg\min_{x} J(x)$
导数
记现在需要优化的函数为 $y = f(x)$,这个函数的导数 $f'(x)$ 表示函数在点 $x$ 处的变化率,或者说是函数图像在该点的切线斜率。
利用导数的定义,发现导数实际指示了函数在该点的变化趋势,我们可以很容易的判断出函数下降的方向
取一个小的正数 $\epsilon$,如果 $f'(x) > 0$,则 $f(x - \epsilon) < f(x)$,否则 $f(x + \epsilon) < f(x)$,也就是说:
$$ f(x -\epsilon\cdot \text{sign}(f'(x))) < f(x) $$因此,导数的负方向是函数下降最快的方向。
梯度
下面,将上面所述的过程扩展到多维空间中,假设现在有一个多变量函数 $f: \mathbb{R}^n \to \mathbb{R}$,其输入为一个 $n$ 维向量 $x = [x_1, x_2, \ldots, x_n]^T$,输出为一个标量 $y = f(x)$。我们希望找到使得 $f(x)$ 最小化的 $x$。
在多维空间中,导数的概念被推广为梯度 (Gradient),梯度是一个向量,包含了函数对每个变量的偏导数,表示为:
$$ \nabla f(x) = \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n} \right]^T $$梯度的每个分量 $\frac{\partial f}{\partial x_i}$ 表示函数 $f$ 对变量 $x_i$ 的变化率,梯度向量指示了函数在点 $x$ 处变化最快的方向。
根据导数部分的结论,我们会认为应该跟着偏导数的方向进行更新。 但是,实际上,我们可以推出,对于一个小的正数 $\epsilon$,$f(x)$ 下降最快的方向恰是 $-\nabla f(x)$,所以有:
$$ f(x - \epsilon \cdot \nabla f(x)) < f(x) $$梯度下降算法
基于上述结论,我们可以设计一个迭代算法来寻找函数的最小值,即每次沿着导数的负方向前进一个小步长,从而逐步逼近函数的最小值。
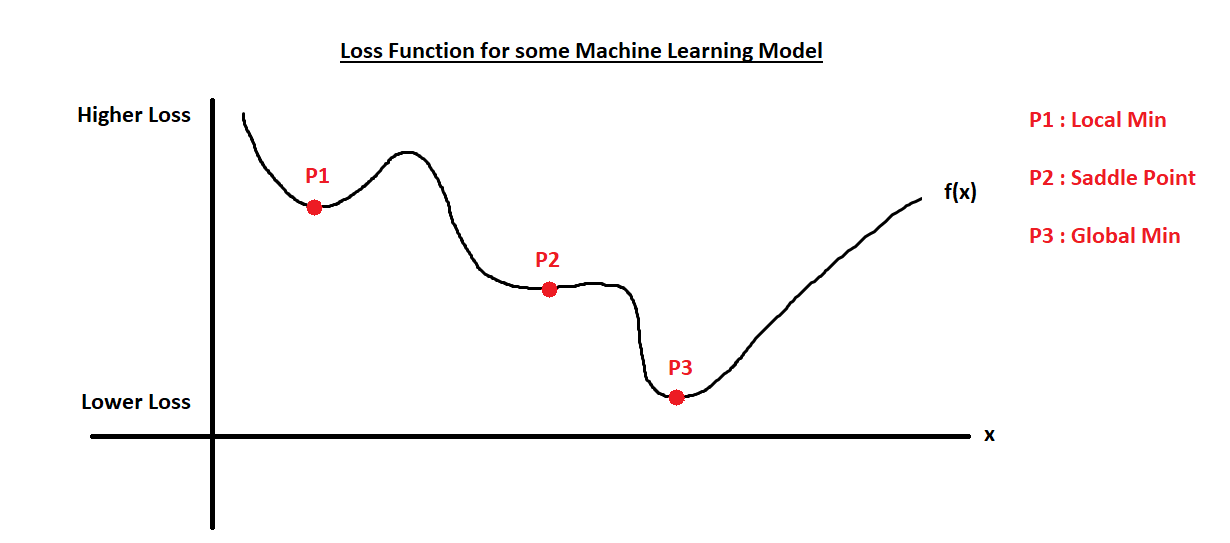
根据导数的性质,$f'(x)=0$ 的点实际并不一定为极小值点。在实际情况下,一般不会进入鞍点(saddle point)。但是,我们找到的极小值点也不一定是全局最小值点,可能只是局部最小值点,且很有可能是局部最小值点。虽然这样,我们仍然接受局部最小值点,因为寻找全局最小值点通常是不可行的,且局部最小值点通常已经足够好。
例如在这张图中,我们很难停在P2这个点上,因为浮点计算误差,很难精确的停在这个点上。但是有很大概率,我们会停在P1这个点上,即使它不是全局最小值点。通常这个点已经足够好了。
扩展到多维空间中,我们可以设计如下的梯度下降算法:
- 初始化参数 $x$,可以随机初始化或者使用某种启发式方法。
- 计算梯度 $\nabla f(x)$。
- 更新参数:$x = x - \alpha \cdot \nabla f(x)$,其中 $\alpha$ 是学习率 (Learning Rate),控制每次更新的步长。
- 重复步骤 2 和 3,直到满足停止条件(例如梯度足够小,或者达到最大迭代次数)。
Learning Rate (学习率)
学习率 $\alpha$ 是梯度下降算法中的一个重要超参数,决定了每次参数更新的步长大小。选择合适的学习率对于梯度下降的收敛速度和最终结果有着显著影响。
- 如果学习率过大,可能会导致参数更新过度,错过最优解,甚至使得目标函数发散。
- 如果学习率过小,收敛速度会非常慢,可能需要大量的迭代才能接近最优解,增加计算成本。 通常,学习率需要通过实验进行调优,可以使用学习率衰减(Learning Rate Decay)等技术来动态调整学习率,以提高收敛效果。在这里暂时不讨论这些技术。